2020-06-17

20ss►安全编程原理

安全编程原理-LAB3-overflow

Lab2.3 Buffer Overflow Vulnerability

1、Disable Address Space Randomization.

2、Create Vulnerable Program

为了方便，使用ftp直接将stack.c上传到虚拟机上。使用cat命令检查文件。

3、 Compile the Vulnerable Program and make it set-root-uid.

由于ubuntu没有root账户，首先创建root账户

接着按照要求进行编译（使用编译选项允许栈运行并且关闭Stack Guard的安全机制）

为了方便，我们加上-m32的编译选项，编译出32位的可执行文件。

4、Complete the vulnerability code.

4-1 使用gdb对stack进行反汇编调试：

disass bof

得到 bof 函数的反汇编结果。根据c语言的堆栈传递参数模式，我们知道 0x8048485 处可以得到函数的返回地址。故在 0x8048485 处设置断点1。调用strcpy函数前面有两个赋值语句，根据c语言函数调用过程可知，第二个赋值是 buffer 的地址。故在 0x08048494 设置断点二。
获取返回的地址

程序运行到断点1

此时 esp 寄存器内的值 = 返回地址 - 4 . 这个4是 push 进来的 ebp

使用i r指令查看，可以知道结果为 0xffffd4a8 + 4 = 0xffffd4ab

即返回地址为 0xffffd4ab
获取 buffer 的地址

程序运行到断点2

此时 eax 寄存器内的值即为 buffer 的地址

可以看到结果为 0xffffd494
计算偏移地址数目

0xffffd4ab - 0xffffd494 = 0x18 =24

因此我们应当将需要跳转的地址放在 buffer+24 处

4-2 完善 exploit.c

将 shellcode 放到 badfile 文件后 0x100 处。则所需跳转的地址为 &buffer + 0x100

  char addr[4] = { 0x94 , 0xd5 , 0xff , 0xff }; //小端规则 实际地址 0xffffd494 + 0x100
                                                //               0xffffd594
  memcpy(buffer+24,addr,4);        
  memcpy(buffer+0x100,code,50);

5、Results

编译运行 exploit 和 stack. 成功进入shell。如下图

6、感悟

本次实验最开始使用64位，但是不太清楚64位的汇编语法，故后使用32位完成了实验
gcc反汇编的mov语句和vc不太相同，需要注意
禁止动态分配内存每次重启都需要设置。

2020-06-10

20ss►安全编程原理

安全编程原理-LAB2-GCC

Running a Hello World Program in C using GCC

一、打开终端

由于直接使用虚拟机的终端界面过小且不清晰，故本实验在windows下使用ssh协议连接到了虚拟机

如图

二、创建`debug_me.c`

保存后检查结果

三、编译运行

输入

1
2
3

gcc -g debug_me.c -o debug_me
gdb debug_me
run "hello, world" "goodbye, world"

出现运行结果：

1 2	String '1' - 'hello,world' String '2' - 'goodbye world'

符合预期结果

调试尝试

设置断点
1
break main
输入run debug_me "hello, world" "goodbye, world"

程序运行到main函数之中
连续几次 n(next的缩写)，运行到 print_string 函数时，输入n 程序直接运行出第一次输出的结果： String ‘1’ - ‘debug_me’
继续调试，程序再次运行到 print_string 函数时，输入 s （step）,我们发现程序进入到了 print_string 函数内部。
step 和 next的区别

step表示单步进入，当当前语句是一个函数时，程序将进入该函数内部

next表示单步运行，当当前语句是一个函数时，程序不会进入到函数内部，而是直接运行出结果。
继续调试，输入where，得到结果

#0 print_string ......

#1 .... in main

  (gdb) frame 0
  (gdb) print i
  ...
  (gdb) frame 1
  (gdb) print i

得到结果

前者 No symbol “i” in current context

后者 $$1 = 2$

2020-06-07

20ss►安全编程原理

安全编程原理-LAB1-MVC

大家都说鸟叔这个课很好，事情干完就可以满，而且能学到一些有意思的东西。

Lab1主要是实践MVC设计模式。这个设计模式在我看来已经过时了，毕竟现在MVVM的框架已经有了诸如React和Vue这种成熟的框架。而且MVVM解耦程度更高。

不过基础还是要夯实，我用MVC的设计方式写了个聊天室。用express框架做后端渲染。写下来感觉还是前后端分离才是新世纪的开放理念。

项目地址： https://github.com/YdreamW/20ss/tree/master/Secure%20Programming/LAB1.1%EF%BC%861.2

2020-05-31

20ss►Linux

Linux-Lab2

Linux的第二次Lab，进行shell命令的实践
见GitHub连接： https://github.com/YdreamW/20ss/blob/master/Linux/shell%E5%91%BD%E4%BB%A4.pdf

2020-05-03

20ss►DBS

DBS-Project4-数据库编程

###实验目的

掌握MySQL数据库函数和存储过程的定义、调用方法
巩固MySQL数据库触发器定义和使用方法
熟悉JDBC连接访问数据库的方法
了解MySQL备份和恢复方法

实验平台

数据库管理系统（MySQL）
pymysql

实验内容和要求

1、建立数据库，并录入数据

该部分内容延用之前的代码，不赘述。

2、函数、存储过程的创建和调用：

使用函数实现统计学生选修课程数量的功能。

代码

delimiter $$
CREATE FUNCTION my_count(NAME VARCHAR(20)) RETURNS INT
DETERMINISTIC
BEGIN
	DECLARE str VARCHAR(5);
	DECLARE a INT;
	SELECT SID FROM S WHERE SNAME=NAME INTO str;
	SELECT COUNT(CID) FROM SC WHERE SID = str INTO a;
	RETURN a;
END
$$
delimiter;
SELECT my_count("Wang feng");

结果

使用存储过程实现查询某个学生选修的课程的总学分。

代码

delimiter $$
CREATE PROCEDURE my_count(IN NAME VARCHAR(20), OUT my_sum INT)
DETERMINISTIC
BEGIN
	DECLARE str VARCHAR(5);
	SELECT SID FROM S WHERE SNAME=NAME INTO str;
	SELECT sum(credit) FROM C WHERE CID in (SELECT CID FROM SC WHERE SID = str) INTO my_sum;
END
$$
delimiter;
CALL my_count("Wang feng",@credits);
SELECT (@credits);

结果

####3、触发器的创建

删除一个学生信息，确保SC中也不存在该学生的信息；

SET foreign_key_checks = 0;
delimiter $$
CREATE TRIGGER s_delete AFTER DELETE ON s FOR EACH ROW
BEGIN
	DELETE FROM SC WHERE SID not in (SELECT SID FROM S);
END
$$
delimiter;

添加选课信息时，确保课程存在。

delimiter $$
CREATE TRIGGER course_insert_check before insert
ON sc FOR EACH ROW
begin
	 declare msg varchar(100);
     if NEW.CID not in (select CID from C)
     THEN
         SET msg = CONCAT('illegal messege');
		SIGNAL SQLSTATE 'HY000' SET MESSAGE_TEXT = msg;
     end if;
end
$$
delimiter ;

4、使用python实现数据库连接访问

代码

import pymysql 

# select all avaliable courses
def show_courses(cursor):
    print('show all courses')
    cursor.execute('select distinct CNAME from C')
    output = cursor.fetchall()
    print(output)

# check a course
def check_course(cursor,sid):
    print('select physics course for' +sid)
    sql = "select * from C where CID not in(select CID from SC where SID = %s);"
    cursor.execute(sql,sid)
    output = cursor.fetchall()
    print(output)
    conn.commit()

#select a course
def select_course(cursor,sid,cid):
    print('select %s course for %s'%(cid,sid))
    cursor.execute('insert into SC (SID, CID, GRADE) values(%s, %s, %s)', ['S3', 'C2', 0])
    output = cursor.fetchall()
    print(output)
    conn.commit()

# select all courses that have been selected
def show_selected_courses(cursor):
    print('show all courses that have been selected')
    cursor.execute('select distinct CNAME from SC natural join C')
    output = cursor.fetchall()
    print(output)

# select all courses that have been selected by someone
def show_selected_courses_by_someone(cursor,sid):
    print('show all courses that have been selected by %s'%(sid))
    cursor.execute('select distinct CNAME from SC natural join C where SID = %s', sid)
    output = cursor.fetchall()
    print(output)

# drop out of a course
def quit_course(cursor,sid,cid):
    print('drop out of the %s course for %s'%(cid,sid))
    sql = "delete from SC where SID =%s and CID = %s;"
    cursor.execute(sql,(sid,cid))
    output = cursor.fetchall()
    print(output)


# connect database
conn = pymysql.connect(host = '127.0.0.1', port = 3306, user = 'root', passwd = '123', db = 'school')
cursor = conn.cursor()

show_courses(cursor)
select_course(cursor,'S2','C2')
show_selected_courses(cursor)
quit_course(cursor,'S2','C2')
show_selected_courses_by_someone(cursor,'S1')

结果

2020-04-30

20ss►Linux

Linux-Lab1

Linux 课程的第一次lab。要求自选课题进行调研。

见Github连接: https://github.com/YdreamW/20ss/blob/master/Linux/lab1-%E7%A0%94%E7%A9%B6%E6%8A%A5%E5%91%8A.pdf

2020-04-02

20ss►DBS

DBS-Project3-SQL数据完整性

实验3-SQL数据完整性

###实验目的

掌握MySQL数据库的完整性约束的定义方法；
掌握MySQL数据库的用户的创建方法。
掌握MySQL数据库的权限设置方法。

实验平台

数据库管理系统（MySQL）

实验内容和要求

1、建立数据库school

1	CREATE DATABASE school;

2、数据的定义

利用create创建三张表,同时增加主键外键约束

CREATE TABLE S (
	SID VARCHAR ( 20 ) ,
	SNAME VARCHAR ( 20 ),
	AGE INT,
	SEX VARCHAR ( 1 ) ,
	PRIMARY KEY (SID)
);
CREATE TABLE C(
	CID VARCHAR ( 20 ) ,
	CNAME VARCHAR(20),
	TEACHER VARCHAR(20),
	PRIMARY KEY (CID)
);
CREATE TABLE SC(
	SID VARCHAR(20),
	CID VARCHAR(20),
	GRADE INT,
	PRIMARY KEY (SID,CID),
	FOREIGN KEY (SID) REFERENCES S(SID) ON UPDATE CASCADE ON DELETE CASCADE,
	FOREIGN KEY (CID) REFERENCES C(CID) ON UPDATE CASCADE ON DELETE CASCADE
);

3、完整性约束设置及其测试

完整性约束设置

1 2	ALTER TABLE S ADD CHECK (sex in ('f','m')); ALTER TABLE S ADD CHECK (0 <= age and age <=200) ;

测试

INSERT INTO S (SID, SNAME, AGE, SEX)
             VALUES ('S1','Wang feng', 20, 'f');
INSERT INTO S (SID, SNAME, AGE, SEX)
             VALUES ('S2','Li feng', 20, 't');
INSERT INTO S (SID, SNAME, AGE, SEX)
             VALUES ('S2','Li feng', -1, 'm');
INSERT INTO S (SID, SNAME, AGE, SEX)
             VALUES ('S2','Li feng', 14, 'm');

运行结果

触发器定义及测试

CREATE TRIGGER student_insert_check BEFORE INSERT
ON s FOR EACH ROW
BEGIN
  DECLARE msg varchar(100);
	IF NEW.age <= 0 OR NEW.age >= 200 
	THEN
		SET msg = CONCAT('您输入的年龄值：',NEW.age,' 为无效的年龄，请输入0到200以内的有效数字。');
		SIGNAL SQLSTATE 'HY000' SET MESSAGE_TEXT = msg;
	END IF;
END;

INSERT INTO S (SID, SNAME, AGE, SEX)
			 VALUES ('S3','Cy', 201, 'f');

结果

外键约束测试

INSERT INTO S (SID, SNAME, AGE, SEX)
			 VALUES ('S1','Wang feng', 20, 'f');
INSERT INTO S (SID, SNAME, AGE, SEX)
			 VALUES ('S2','Li feng', 20, 't');
INSERT INTO S (SID, SNAME, AGE, SEX)
			 VALUES ('S2','Li feng', -1, 'm');
INSERT INTO S (SID, SNAME, AGE, SEX)
			 VALUES ('S2','Li feng', 14, 'm');
INSERT INTO C (CID, CNAME, TEACHER)
       VALUES ('C1', 'DB', 'Li');
INSERT INTO C (CID, CNAME, TEACHER)
       VALUES ('C2', 'maths', 'Ma');
INSERT INTO SC (SID, CID , GRADE)
       VALUES ('S1','C1',70);
INSERT INTO SC (SID, CID , GRADE)
       VALUES ('S2','C1',81);
INSERT INTO SC (SID, CID , GRADE)
       VALUES ('S1','C2',65);
SELECT * FROM SC;
DELETE FROM S WHERE SID = 'S2' ;
SELECT * FROM SC;

结果

3、MySQL上的用户和权限的设置

CREATE USER 'test1'@'localhost' IDENTIFIED by '123';
CREATE USER 'test2'@'localhost' IDENTIFIED by '123';
GRANT INSERT,UPDATE ON school.C TO 'test1'@'localhost' WITH GRANT OPTION;

revoke update on school.C from 'test1'@'localhost';
show grants for 'test2'@'localhost';
Drop user 'test2'@'localhost';

2020-03-29

20ss►ADS

ADS-project1-斐波那契堆优化的最短路径算法

源代码地址： https://github.com/YdreamW/20ss/tree/master/ads/project1_Fibheap%26ShortestPath

题目要求

Shortest path problems are ones of the most fundamental combinatorial optimization problems with many applications, both direct and as subroutines in other combinatorial optimization algorithms. Algorithms for these problems have been studied since 1950’s and still remain an active area of research.

In this project you are supposed to compute the shortest paths using Dijkstra’s algorithm. The implementation shall be based on a min-priority queue, such as a Fibonacci heap. The goal of the project is to find the best data structure for the Dijkstra’s algorithm.

Your tasks are:

(1) Implement the algorithm with at least two different heap structures, while Fibonacci heap must be one of them.
(2) Use the USA road networks for evaluation. The data sets can be downloaded from http://www.dis.uniroma1.it/challenge9/download.shtml which provides the benchmarks for the 9th DIMACS Implementation Challenge. (Note: you must only list the download links of these test data sets instead of uploading them with your reports.)
(3) At least 1000 pairs of query are required in evaluating the run times of the algorithm with various of implementations.

###Grading Policy:

Programming: Implement Dijkstra’s algorithm with Fibonacci heap and other heaps (6 pts.). Write a test of performance program (3 pts.). All the codes must be sufficiently commented.

Testing: Provide the necessary inputs for testing and give the run time table (2 pts.). Plot the run times vs. input sizes for illustration (2 pts.). Write analysis and comments (3 pts.).

Documentation: Chapter 1 (1 pt.), Chapter 2 (2 pts.), and finally a complete report (1 point for overall style of documentation).

斐波那契堆: (参考:斐波那契堆)

斐波那契堆(Fibonacci heap)是堆中一种，它和二项堆一样，也是一种可合并堆；可用于实现合并优先队列。斐波那契堆比二项堆具有更好的平摊分析性能，它的合并操作的时间复杂度是O(1)。
与二项堆一样，它也是由一组堆最小有序树组成，并且是一种可合并堆。
与二项堆不同的是，斐波那契堆中的树不一定是二项树；而且二项堆中的树是有序排列的，但是斐波那契堆中的树都是有根而无序的。

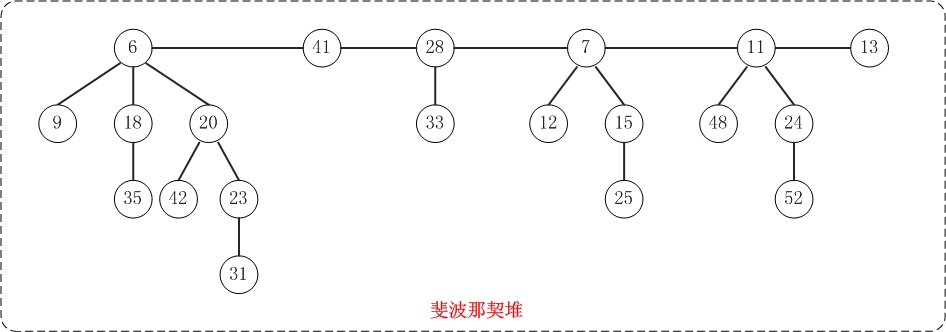
基本定义

FibNode是斐波那契堆的节点类，它包含的信息较多。key是用于比较节点大小的，degree是记录节点的度，left和right分别是指向节点的左右兄弟，child是节点的第一个孩子，parent是节点的父节点，marked是记录该节点是否被删除第1个孩子(marked在删除节点时有用)。

FibHeap是斐波那契堆对应的类。min是保存当前堆的最小节点，keyNum用于记录堆中节点的总数，maxDegree用于记录堆中最大度，而cons在删除节点时来暂时保存堆数据的临时空间。

下面看看斐波那契堆的内存结构图。

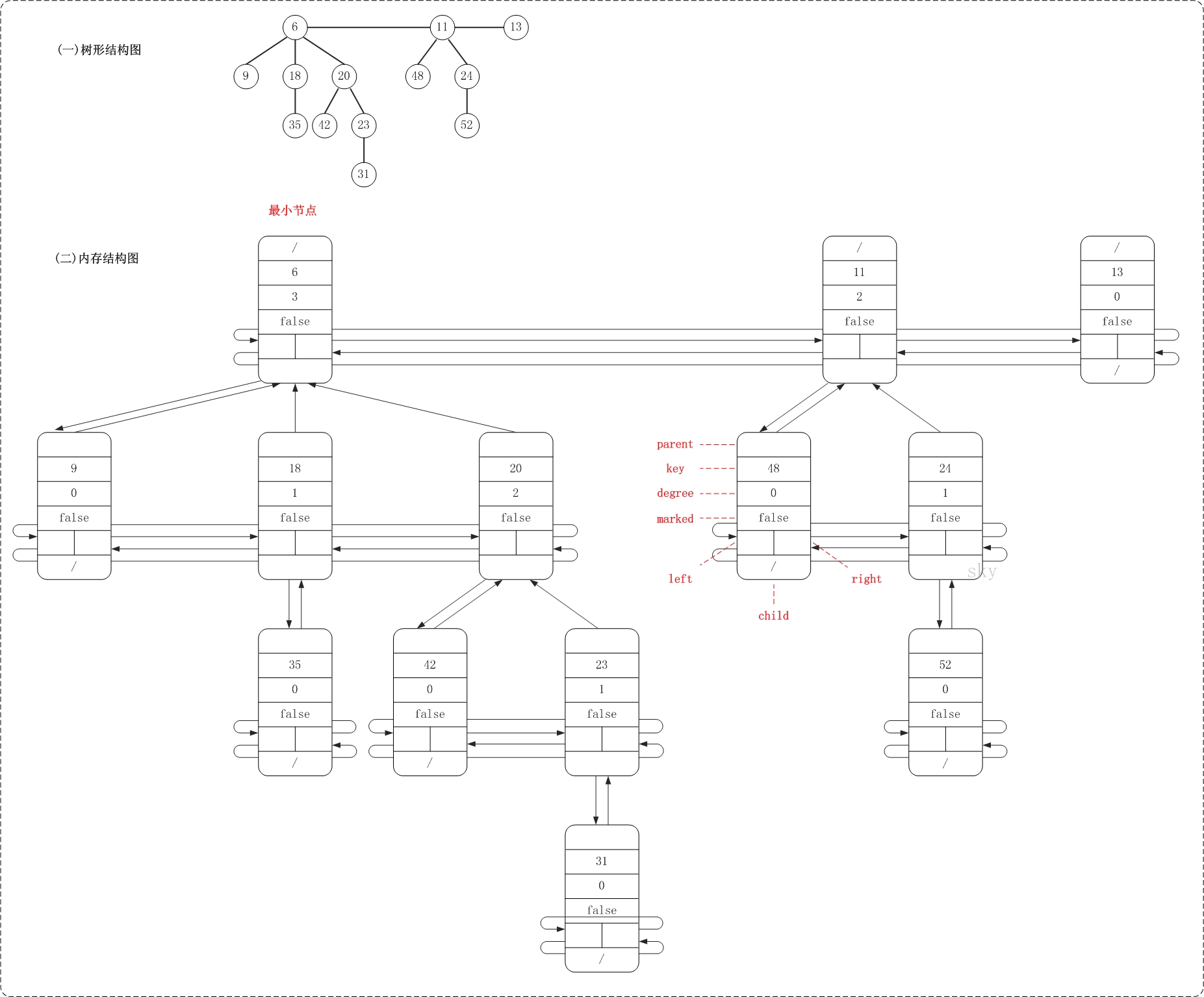
从图中可以看出，斐波那契堆是由一组最小堆组成，这些最小堆的根节点组成了双向链表(后文称为”根链表”)；斐波那契堆中的最小节点就是”根链表中的最小节点”！

插入操作

插入操作非常简单：插入一个节点到堆中，直接将该节点插入到”根链表的min节点”之前即可；若被插入节点比”min节点”小，则更新”min节点”为被插入节点。

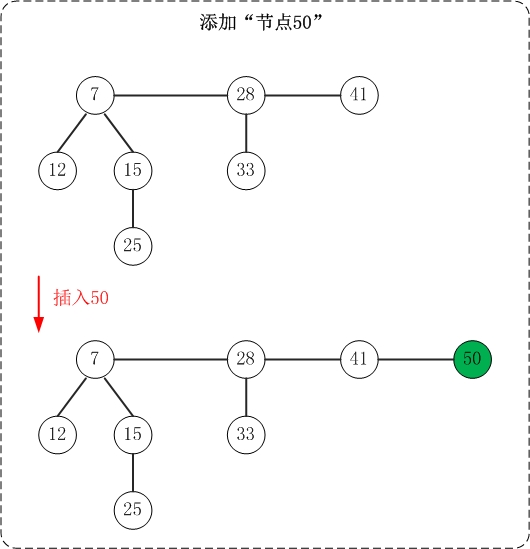
上面是插入操作的示意图。

斐波那契堆的根链表是”双向链表”，这里将min节点看作双向联表的表头(后文也是如此)。在插入节点时，每次都是”将节点插入到min节点之前(即插入到双链表末尾)”。此外，对于根链表中最小堆都只有一个节点的情况，插入操作就很演化成双向链表的插入操作。

合并操作

合并操作和插入操作的原理非常类似：将一个堆的根链表插入到另一个堆的根链表上即可。简单来说，就是将两个双链表拼接成一个双向链表。

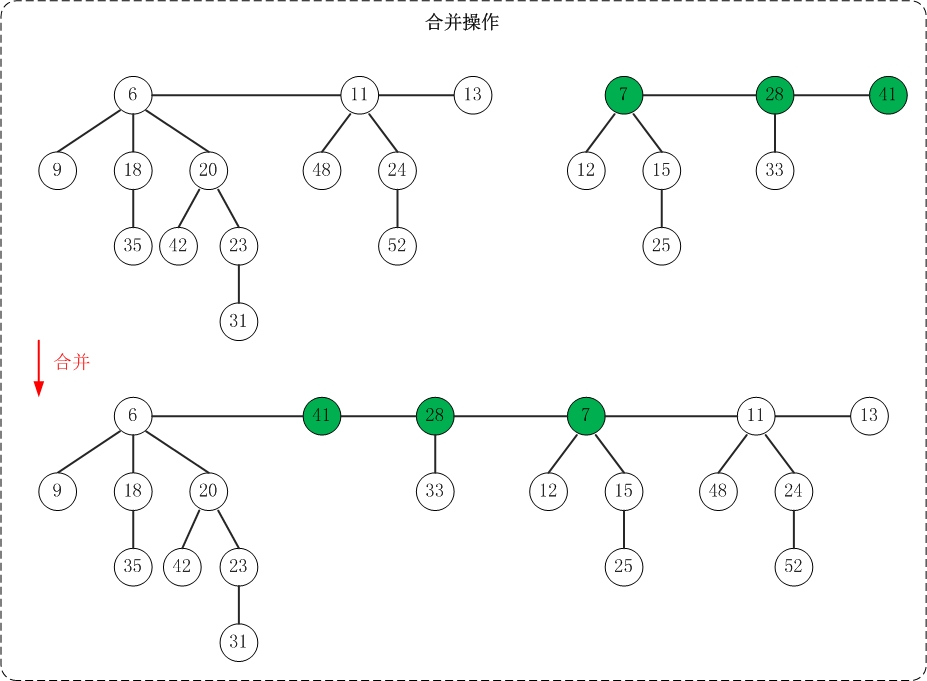
取出最小节点

抽取最小结点的操作是斐波那契堆中较复杂的操作。
(1）将要抽取最小结点的子树都直接串联在根表中；
(2）合并所有degree相等的树，直到没有相等的degree的树。

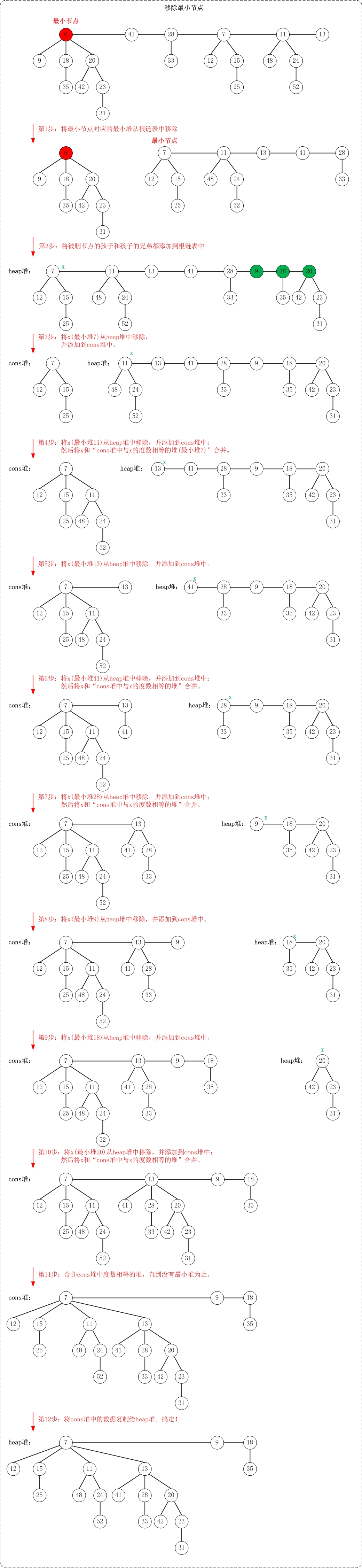
上面是取出最小节点的示意图。图中应该写的非常明白了，若有疑问，看代码。

减小节点值

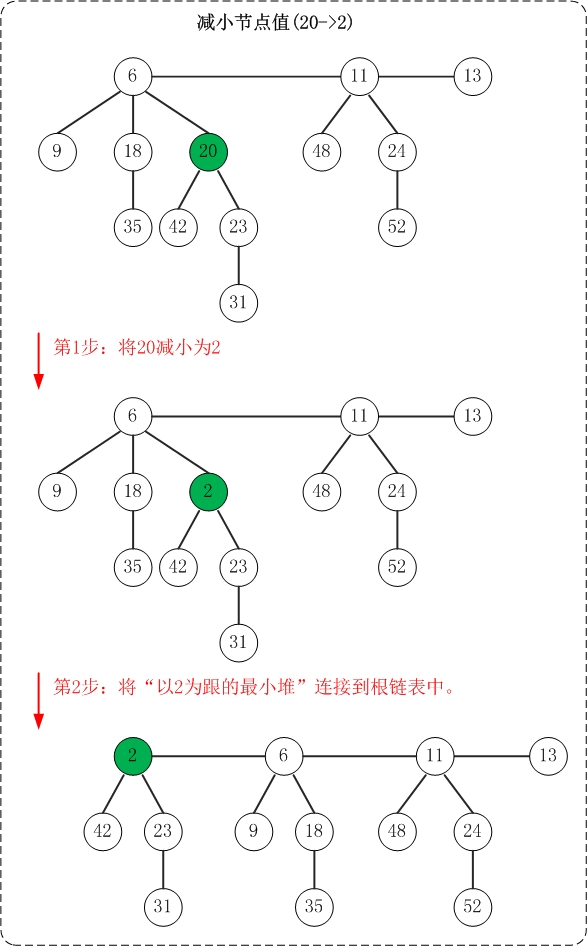
减少斐波那契堆中的节点的键值，这个操作的难点是：如果减少节点后破坏了”最小堆”性质，如何去维护呢？下面对一般性情况进行分析。
(1) 首先，将”被减小节点”从”它所在的最小堆”剥离出来；然后将”该节点”关联到”根链表”中。倘若被减小的节点不是单独一个节点，而是包含子树的树根。则是将以”被减小节点”为根的子树从”最小堆”中剥离出来，然后将该树关联到根链表中。
(2) 接着，对”被减少节点”的原父节点进行”级联剪切”。所谓”级联剪切”，就是在被减小节点破坏了最小堆性质，并被切下来之后；再从”它的父节点”进行递归级联剪切操作。
而级联操作的具体动作则是：若父节点(被减小节点的父节点)的marked标记为false，则将其设为true，然后退出。
否则，将父节点从最小堆中切下来(方式和”切被减小节点的方式”一样)；然后递归对祖父节点进行”级联剪切”。
marked标记的作用就是用来标记”该节点的子节点是否有被删除过”，它的作用是来实现级联剪切。而级联剪切的真正目的是为了防止”最小堆”由二叉树演化成链表。
(3) 最后，别忘了对根链表的最小节点进行更新。

增加节点值

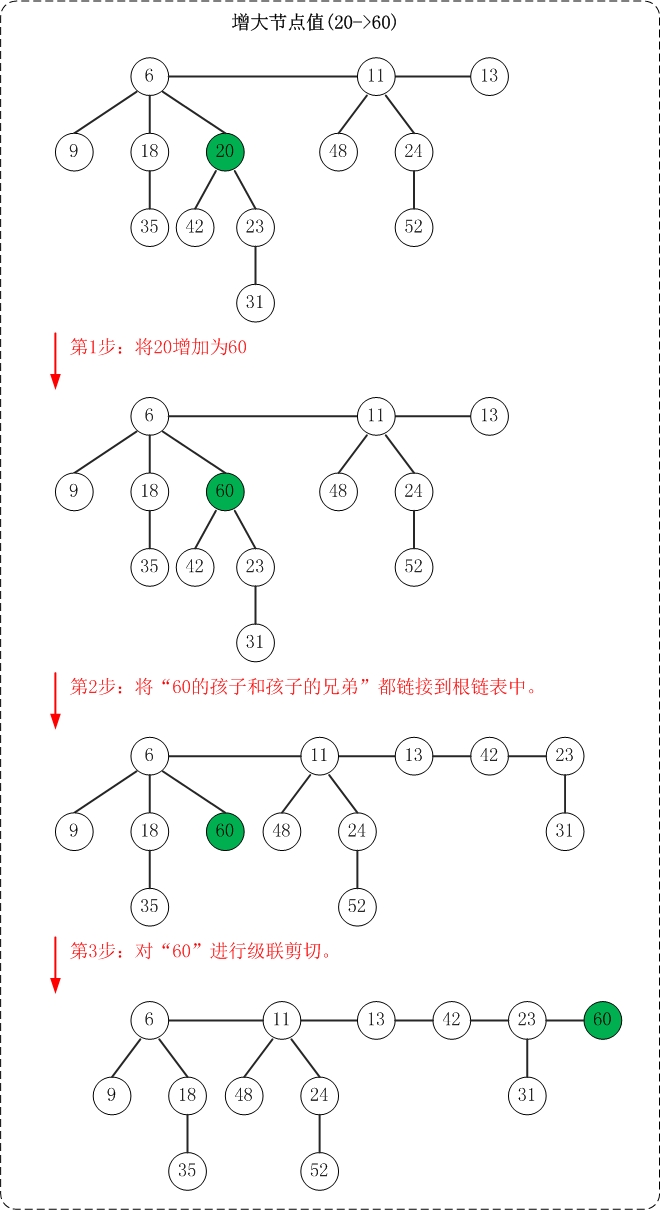
增加节点值和减少节点值类似，这个操作的难点也是如何维护”最小堆”性质。思路如下：
(1) 将”被增加节点”的”左孩子和左孩子的所有兄弟”都链接到根链表中。
(2) 接下来，把”被增加节点”添加到根链表；但是别忘了对其进行级联剪切。

删除节点

删除节点，本文采用了操作是：”取出最小节点”和”减小节点值”的组合。
(1) 先将被删除节点的键值减少。减少后的值要比”原最小节点的值”即可。
(2) 接着，取出最小节点即可。

2020-03-21

20ss►DBS

DBS-Project2-SQL数据定义和操作

实验2-SQL数据定义和操作

###实验目的

掌握MySQL数据库的复杂SQL查询和DML语句的使用方法
掌握MySQL数据库的视图设计和使用方法。
掌握MySQL数据库的索引设计和使用方法。

实验平台

数据库管理系统（MySQL）

实验内容和要求

1、建立数据库school

1	CREATE DATABASE school;

2、数据的定义

利用create创建三张表。

CREATE TABLE IF NOT EXISTS S(
	SID VARCHAR(20) not NULL,
	SNAME VARCHAR(20) not NULL,
	AGE INT UNSIGNED,
	SEX VARCHAR(1)
);
CREATE TABLE IF NOT EXISTS SC(
	SID VARCHAR(20) not NULL,
	CID VARCHAR(20) not NULL,
	GRADE INT UNSIGNED
);
CREATE TABLE IF NOT EXISTS C(
	CID VARCHAR(20) not NULL,
	CNAME VARCHAR(20) not NULL,
	TEACHER VARCHAR(20) not NULL
);

用alter 增加主键和外键

ALTER TABLE S ADD PRIMARY KEY (SID);
ALTER TABLE SC ADD PRIMARY KEY (SID,CID);
ALTER TABLE C ADD PRIMARY KEY (CID);
ALTER TABLE SC ADD FOREIGN KEY (SID) REFERENCES S (SID);
ALTER TABLE SC ADD FOREIGN KEY (CID) REFERENCES C (CID);

3、数据插入

代码略

插入结果如下

4、数据查询

```mysql
SELECT DISTINCT SNAME, AGE FROM S;
SELECT DISTINCT SID FROM SC;
SELECT DISTINCT SID FROM SC WHERE GRADE < 60;
SELECT DISTINCT SNAME, SEX , AGE FROM S WHERE AGE BETWEEN 20 AND 23;
SELECT DISTINCT SID, SNAME, AGE FROM S WHERE SNAME LIKE ‘liu%’;
SELECT MAX(GRADE) FROM SC WHERE CID = ‘C1’;
SELECT CID, COUNT(SID) FROM SC GROUP BY CID;
SELECT DISTINCT SNAME FROM S NATURAL JOIN SC WHERE SC.CID = ‘C3’;
SELECT DISTINCT SNAME FROM S NATURAL JOIN SC WHERE SC.CID = ‘C1’ and SC.GRADE > 90;
SELECT CID, AVG(GRADE) FROM SC GROUP BY CID;
SELECT DISTINCT CNAME FROM C WHERE TEACHER LIKE ‘%i%’;
SELECT SID, CID FROM SC WHERE GRADE BETWEEN 80 and 90;
SELECT

  CNAME, MAX( GRADE ) 
  FROM
      SC
  NATURAL JOIN C 
  GROUP BY
      CNAME 
  HAVING
      MAX( GRADE ) > 80;

SELECT

  SID,SNAME,AGE,SEX

FROM

  (
      S
      NATURAL JOIN ( SELECT * FROM SC WHERE CID = 'C1' ) AS T1
      NATURAL JOIN ( SELECT CID, AVG( GRADE ) AS avg FROM SC GROUP BY CID ) AS T2 
  )

WHERE

  GRADE > avg;


	

- 结果展示

	a. ![image-20200320225619693](./DBS-Project2-SQL数据定义和操作/image-20200320225619693.png)

	b. ![image-20200320225632891](./DBS-Project2-SQL数据定义和操作/image-20200320225632891.png)

	c. ![image-20200320225649058](./DBS-Project2-SQL数据定义和操作/image-20200320225649058.png)

	d. ![image-20200320225655825](./DBS-Project2-SQL数据定义和操作/image-20200320225655825.png)

	e. ![image-20200320225702410](./DBS-Project2-SQL数据定义和操作/image-20200320225702410.png)

	f. ![image-20200320225708522](./DBS-Project2-SQL数据定义和操作/image-20200320225708522.png)

	g. ![image-20200320225714513](./DBS-Project2-SQL数据定义和操作/image-20200320225714513.png)

	h. ![image-20200320225720273](./DBS-Project2-SQL数据定义和操作/image-20200320225720273.png)

	i. ![image-20200320225733498](./DBS-Project2-SQL数据定义和操作/image-20200320225733498.png)

	j. ![image-20200320225756334](./DBS-Project2-SQL数据定义和操作/image-20200320225756334.png)

	k. ![image-20200320225828417](./DBS-Project2-SQL数据定义和操作/image-20200320225828417.png)

	l. ![image-20200320225838289](./DBS-Project2-SQL数据定义和操作/image-20200320225838289.png)

	m. ![image-20200320225844874](./DBS-Project2-SQL数据定义和操作/image-20200320225844874.png)

	n. ![image-20200320225852895](./DBS-Project2-SQL数据定义和操作/image-20200320225852895.png)

##### 5、视图使用

- ```mysql
	CREATE VIEW S_C_SC as SELECT SID, SNAME, CNAME, GRADE FROM S NATURAL JOIN SC NATURAL JOIN C;
	SELECT * FROM S_C_SC;
	SELECT CNAME, GRADE FROM S_C_SC WHERE SNAME LIKE 'Wu%';
	UPDATE S_C_SC SET SNAME = 'Hello' WHERE SID = 'S1';
	SELECT * FROM S_C_SC;
	SELECT * FROM S;
	UPDATE S_C_SC SET SNAME = 'Wang feng' WHERE SID = 'S1';
	DROP VIEW S_C_SC;

结果展示

6、索引的使用

```mysql
SHOW INDEX FROM C;
ALTER TABLE C ADD INDEX INDEX_CID(CID);
SHOW INDEX FROM C;
DROP INDEX INDEX_CID ON C;


-   结果展示

	- 

	![image-20200321225603246](./DBS-Project2-SQL数据定义和操作/image-20200321225603246.png)

	- ![image-20200321225717407](./DBS-Project2-SQL数据定义和操作/image-20200321225717407.png)

	- 

- 索引的使用可以提升查找数据的速度，不会改变表中数据



##### 7、数据更新

- ```mysql
	UPDATE C SET CID = 'C6' WHERE CID = 'C3';

报错信息

1	1451 - Cannot delete or update a parent row: a foreign key constraint fails (`school`.`sc`, CONSTRAINT `sc_ibfk_2` FOREIGN KEY (`CID`) REFERENCES `c` (`CID`))

```mysql
SET FOREIGN_KEY_CHECKS = 0;
UPDATE C SET CID = ‘C6’ WHERE CID = ‘C3’;
SET FOREIGN_KEY_CHECKS = 1;


	   禁用外键约束即可删除

- 题目中 “用update命令修改sc表中课由“Li”任课的课程号为由“Wen”任课的课程号” 要求会导致主键重复，故删除了改条数据

- ```mysql
	SET FOREIGN_KEY_CHECKS = 0; 
	UPDATE C SET CID = 'C6' WHERE CID = 'C3';
	SET FOREIGN_KEY_CHECKS = 1;
	DELETE FROM SC WHERE SID = 'S3' AND CID = 'C1';
	UPDATE SC NATURAL JOIN C SET SC.CID = (SELECT CID FROM C WHERE TEACHER = 'Wen') WHERE C.TEACHER = 'Li' ;
	DELETE FROM SC WHERE GRADE < 60;
	DELETE SC FROM SC NATURAL JOIN C WHERE C.CNAME = 'OS';
	SELECT * FROM SC;

8、删除表和数据库

1 2	DROP TABLE S,C,SC; DROP DATABASE school;

2020-03-02

20ss►DBS

DBS-Project1-DBMS的安装与使用

#实验1 DBMS的安装和使用

实验目的

通过安装某数据库管理系统(MySQL)，初步了解DBMS的运行环境
了解DBMS交互界面、图形界面和系统管理工具的使用
搭建实验平台

实验平台

操作系统
数据库管理系统：MySQL
DBMS图形界面：Navicat （说明：由于之前使用过该可视化软件，故没有再下载MySQL Workbench）

实验内容和要求

根据官方文档，安装DBMS

由于在上此课程之前的开发过程中已经安装使用过MySQL，因此DBMS的安装过程不作展示

如图，MySQL登录成功。
了解DBMS的用户管理

上图中使用了root用户进行登录数据库，root用户的操作权限最高，可以对数据库进行任意的操作。如果所有想要登录数据库的用户都使用root进行登录，无疑是存在安全隐患的。所以MySQL具有用户的管理系统。

MySQL的用户信息保存在数据库mysql的数据表user中。
- 查看数据表user
  
  输入以下命令，我们可以得到mysql>user 的表结构
  1
  2
  use mysql
  describe user
  输入以下命令
  1
  select host,user,password from user
  可以得到目前mysql 的用户信息
  
  可以看到第一条信息就是 root@localhost 也就是我们刚刚登录所使用的用户。密码字段的内容是加密后的密文。
- 创建新用户
  
  输入命令
  1
  create user create user 'Ydream'@'localhost' identified by 'password';
  这样就创建了一个新的用户
  
  再次输入
  1
  2
  select host,user,password from user
  可以看到user表中新增一条信息，就是刚刚创建的新用户。
  
  退出MySQL后尝试使用新用户登录
  
  登录成功！
  
  尝试查看数据库
  
  发现没有权限。
  
  需要root为Ydream用户设置各种权限，本次实验没有深入研究。
熟悉基本的交互命令
- 查看已有的数据库：
  1
  show databases;
- 创建数据库
  1
  create database name
- 选择某个数据库
  1
  use mysql;
- 查看数据库有哪些表
  1
  show tables;
熟悉图形界面的功能和操作

连接> 新建连接

数据库展示如下图

数据库mysql下的表

表user下的数据

更改表中的值